You see a silhouette of a three-dimensional shape. The silhouette is a circle. Then, you turn to get another view. The new silhouette is still a circle, so you turn again. And again. Every time you look at the shape, you see a circular outline.
Is it a sphere?
In my son’s math book, in the geometry section, there was one question like this. He was given the top, side and front view of an object, and asked “what shape is this?”
The front, top and side views were all circles.
Clearly, the correct answer – for elementary school level math – is that the shape is a sphere. However, like many things in elementary school math, the correct answer is a lie, a simplification made to make the subject simpler to teach.
To show him this, I cooked up the shape shown below.
I’ve shown, here, the front view, top view and side view of the shape. All three views are circles. Is the shape a sphere?
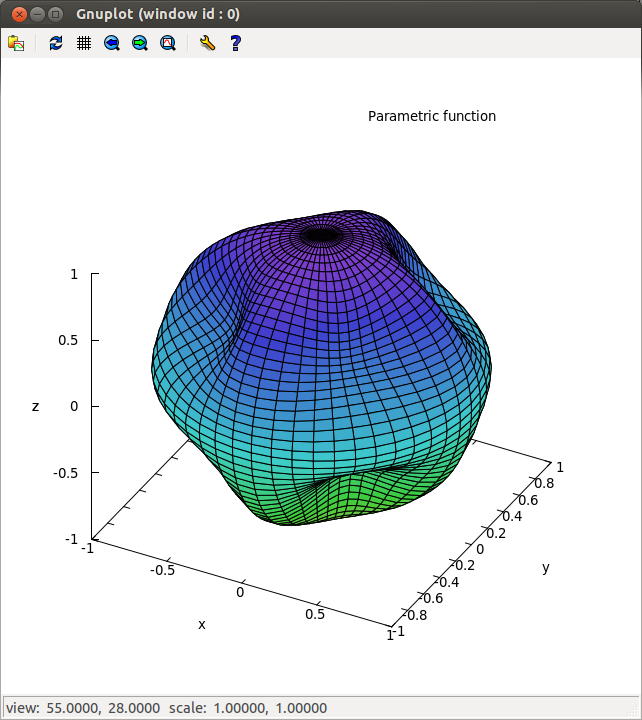
Probably, the shading gave the game away. Here’s the same shape, viewed from a different angle:
Clearly, this is not a sphere. The elementary-school math book has simplified things, as, perhaps, it must.
So, clearly three views is not enough to be sure the shape is a sphere. Would four views help? Five? How many more do we need?
Imagine the shape was a sphere. Each view gives me information about the sphere’s outline, as seen from one direction. The edge of the silhouette carves a great circle around the ball.
Alas, no matter how many circles are drawn, there will still be points on the surface of the sphere that I have not seen. You can then gouge the surface of the sphere – or even, to an extent, fill it out, as long as you don’t touch the disks I’ve seen.
So, to be truly sure you’re looking at a sphere, you need to see it from an infinite number of angles.
Think about that next time you’re looking at some architectural drawings. Will this house be as it seems, or are there hidden Hogwarts-like passages and rooms hidden out of view?