Puzzle : How many triangles can you see in the figure below?
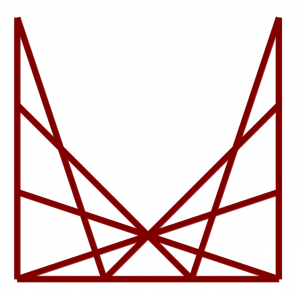
One way to get the answer right is to close your eyes and say “None! I can’t see any!”
On the other hand, maybe you want to get into the spirit of the puzzle, and actually count the triangles. Go on, try now!
If you’re like me, you started by scouring the diagram, hunting for triangles. Trying to combine the little quandrangles together in your head, and keeping track of how many you’d found. Gradually, doubts started creeping in – have I missed any? Have I already counted that one? Is there a better way to do this?
Well, there is. A triangle has three sides, remember? So instead of finding the triangles directly, you could find triplets of lines. They’ll make a triangle if they all meet each other, but at different points. So, go ahead and label the lines. Label them A, B, C, ….
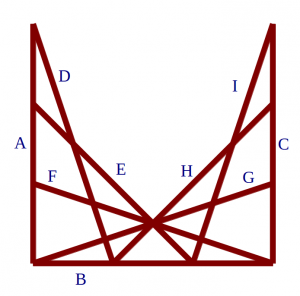
Great! Now, to find a triangle we need to find a triplet of lines that meet at three different points. We could call this a “theorem” – it’s a statement of a mathematical truth (like Pythagoras’ Theorem). We could try to prove the theorem, like so :
- A triangle has three edges, and three corners. The edges each are part of a different line, and the corners are the places the lines meet. Therefore, each triangle matches a set of three lines which meet at three different points.
- Also, if you find three lines meeting at three different points, you can join the points together to get a triangle.
However, it’s much more fun to actually use the theorem. And we’ll use it to count the triangles in the figure above. There are 9 lines. First, note that
- Some pairs of lines don’t meet. Rather than list them all in words, I’ve “listed” them all in a diagram :
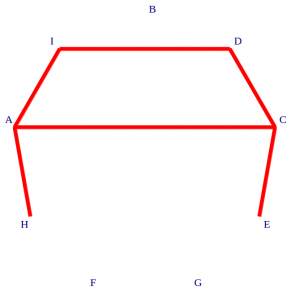
In the diagram, I’ve drawn a red line between A and H, because lines A and H don’t meet. Therefore, I can’t include both A and H in a triple of lines when I’m counting. On the other hand, there’s no red arc between H and C, so that would be fine.
Also :
- E, F, G and H all meet at the same point, so I can’t make a triangle by choosing three of those four lines. For the same reason, I can’t make AGB, BCF, BDH and BEI.
Let’s start counting. It pays to do it systematically.
- With A&B, we could have D, E or F. We can’t have G, because A, G and B all meet at the same point. We can’t have H or I, since they don’t meet A. That’s 3 triples of lines.
- We can’t have A&C
- With A&D, we could have E, F or G. (We’ve already counted ABD, and neither H nor I go with A) That’s 3 more triples.
- With A&E, we could have F and G. That’s two more triples.
- To A&F, we can only add G, that’s one more triple.
- Finally, although A&G can go together, we can’t add H or I to the pair, so there are no more triples involving A.
That’s 3+0+3+2+1= 9 triples – that is, triangles – that use A.
Then, we can count the triples that use B (but not A)
- Starting with B&C, we can’t add D (line D doesn’t meet C) or E (same reason) or F (B, C and F meet at the same place), but we do get triples BCG, BCH and BCI.
- Starting with B&D, we get another 3 triples.
- Starting with B&E, we get another 2 triples
- and so on.
I counted 3+3+2+3+2+1 = 14 triples of lines (trangles) using B. How many did you get?
Then, I got 6 triples starting with C, 6 starting with D, 3 with E, 2 with F and just the one triple (GHI) starting with G. That’s 9+14+6+6+3+2+1 = 41 triangles.
I found it really useful to write a table A to G down the side, B to H along the top, and in each cell write the number of triangles (triples) I found starting with each pair of lines. I also found it more useful, while counting triples of lines, to keep my eye on the original puzzle, rather than on all the analysis and graphs! I also (confess, confess!) got the wrong answer at least two or three times before I got 41. Perhaps you’d like to check my working out more carefully?
Anyway, if you want to challenge your friends, here’s some facebook-friendly versions of the puzzle. Click the puzzle you like to get a larger version, download, then post to FB/G+/Twitter!


nice