John Nash has died, aged 86.
John Nash is most famous for his work on game theory. Game theory tries to understand, mathematically, how people behave in situations where they have to compete or cooperate with another person, like “Rock Scissors Paper”, getting kids to go to bed, house auctions or nuclear disarmament negotiations.
John Nash won the Nobel Memorial Prize in Economic Sciences for his work in the area. Ironically, his greater mathematical accomplishments were in other areas (differential equations and differential geometry). There’s no Nobel Prize in Mathematics, but John Nash received the Abel Prize, which is pretty much just as good, only last week.
My son challenged me to a game of Rock Scissors Paper the other day. He was confident he had a method for winning. However, I had a tool up my sleev that he didn’t – I knew something of John Nash’s methods, and knew how to apply them to Rock Scissors Paper. I could guarantee that neither he nor I would do better than break even, in the long run.
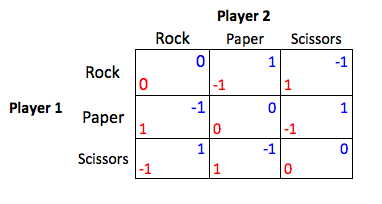
To apply John Nash’s methods, you need to write out a table, showing all the payoffs for every possible play by you and you opponent. The payoffs should be numbers – how much each outcome is worth – in points, dollars, acres or warm fuzzies. For Rock Scissors Paper, the table is shown below. The payoffs for Player 1 are in red, for Player 2 are in blue.
Suppose I’m player 1, and I devise a strategy. Unfortunately for me, you are a superintelligence able to predict my every thought. If my strategy selects Rock, you will outthink me and choose Paper. Likewise, you will win if my strategy says to choose Paper, or to choose Scissors. It seems I am doomed. Except, John Nash gave me a trump card up my sleeve – my strategy was to choose randomly, to assign probabilities for me to choose Rock, Scissors or Paper, and instead of trying to outthink my son, to choose my move in an unpredictable way, using a true source of randomness.
For Rock Scissors Paper, the best probability distribution is to make the probability of each play equal. Then, even a superintelligence cannot outplay me, except by luck.
So that’s what I did. Sure enough, my son’s strategy failed. As it happened, I won, but that was just luck.
If the numbers in the payoff table were different, I could use John Nash’s methods to recalculate the probabilities, and still find an unbeatable strategy. The calculations are not harder than a bright high school student could do.
The important insight here is that sometimes the best strategy is to act randomly. That’s why in elections, and in international politics, you sometimes see the rise of a “maverick”, a player who appears to act a bit crazy, randomly, unpredictably. John Nash’s work suggests that perhaps the mavericks aren’t crazy at all, but have figured out an optimal strategy that avoids losses. Perhaps they are the savvy ones, more than the politicians who clearly state their positions and stick to them through thick and thin.
Rest in Peace, John Nash. John and his wife were on their way back from the airport, having returned from Norway where John had received the Abel prize. Nobody else in the accidentwas even seriously injuries, but John and his wife were flung from the vehicle and died.
Rest in Peace, John Nash. And for the rest of us, buckle up in the car. Game theory suggests that seatbelts are part of the optimal strategy, when playing against fate on the interstate.