The “standard” way to add (or subtract) fractions is to put them over a common denominator first. So, the fraction problem
is
Often, the denominators have no common factor (except 1), so putting the fractions over a common denominator means multiplying top and bottom of each fraction by the denominator of the other.
is
This is a simpler rule to remember, and also works when the denominators do have a common factor.
is
So that’s a fine method to use, and (I believe) kids will often figure out this simpler method, and use it in favor of the “standard” method of finding the “best” common denominator first. I know my son did. This method causes problems, however, when the denominators have a big common factor.
is
which is too hard. Well, harder than it needs to be. After all, who wants to work out 80 x 60 or 11×80+13×60 when they don’t actually need to?
If you know someone who uses this method (and sometimes gets big numbers to multiply), then there’s good news. They can still use their method, with just a small tweak, there’ll be no more multiplying big numbers unless absolutely necessary.
The key is that 60 and 80 have a low common multiple, namely 240. Now, 240=4×60 and 240=3×80. Let’s call the numbers 4 and 3 the cofactors of 60 and 80. Why Cofactors? Because 60 x 4 = 240, so 4 and 60 go together as factors of 240. Likewise, 3 and 80 are factors “together” of 240. Because 3 goes “together” with 80 in some sense, cofactor is a good name.
{Puzzle : can you find a number, and a factor of that number which is its own cofactor?}
Now, back to the fraction addition question. To work out
We don’t have to multiply 80 by 60, or 60 by 80, we just have to multiply 80 by its cofactor (3), and 60 by its cofactor (4). So we get
Multiplying top and bottom of each fraction by a cofactor of the denominator will make the denominators of the two fractions the same. So by slightly modifying the method (changing “multiply by the denominator of the other fraction” to “multiply by the cofactor of this fraction”) you get back to the “standard” method, without the need to completely change the student’s thinking.
If the word “cofactor” is confusing, don’t bother with it. I used it because “the cofactor of 60” is shorter than “the number you multiply 60 by to get the low common multiple you’ve noticed 60 and 80 to have”.
You don’t actually have to find the lowest common multiple for this method to work. If I found the common multiple 480 instead of 240, the cofactors of 60 and 80 would be 8 and 6, and the fraction sum would be
The numbers involved get slightly larger, and there’s a bit more simplifying to do at the end, but it will still get the correct answer without too much trouble.

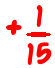

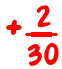

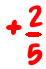
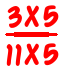
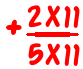
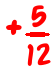
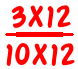
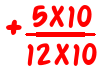

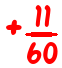
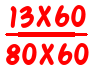
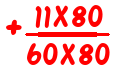

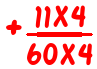
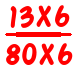
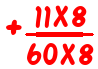
Dr Mike’s Math Games for Kids liked this on Facebook.
Great tip. I worked it into my fraction word problems section. I’ll reference your site when writing my next section on this. http://www.mathworksheetsland.com/5/13fracaddsub.html
Thanks!