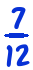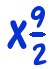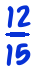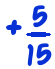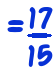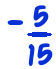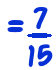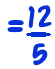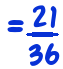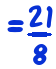The classic way to teach fraction division is like this. To work out, say,
we ‘turn the second fraction upside-down’, to get
and then the division question becomes a multiplication question.
I’ve been watching my son do a whole bunch of fractions questions lately, and a couple of thoughts crossed my mind. First of all, this method will confuse some students. Secondly, there’s another way to do fraction division.
With fraction arithmetic, we give the students procedures for working out various sums. For addition and subtraction, ‘put the fractions over a common denominator’. For multiplication, ‘multiply the top and bottom’. For division, ‘convert it to a multiplication problem’. Ideally, kids would know these methods and the reasons why they work. However, faced with the limited time available in a lower school classroom (and the limited attention span of a typical lower school pupil), I guess a teacher can consider him/herself lucky if an average student just learns the procedures.
In any case, it’s easier to test if a student can solve fractions problems than to test if they understand fractions.
If we teach
- For addition and subtraction, put the fractions over a common denominator and combine
- For multiplication, multiply top and bottom
- For division, turn the second fraction upside down, then multiply
then
- we are teaching three procedures for four operations
- the procedure for division is hard to justify without appealing to a deeper understanding of fractions than most kids will have obtained.
At least the idea of putting things over a common denominator can make sense without too much trouble, as well the way you need to combine the fractions afterwards. For example
- If you have 12 oranges, and add 5 oranges, how many oranges do you have? 17 oranges.
- If you have 12 fifteenths, and add 5 fifteenths, how many fifteenths do you have? 17 fifteenths. So,
Subtraction is similar –
- If you have 12 apples, and take away 5 apples, how many apples do you have? 7 apples.
- If you have 12 fifteenths, and take away 5 fifteenths, how many fifteenths do you have? 7 fifteenths. So,
Is there any reason not to use the same approach for division?
- If you have 12 pizzas, and share them into groups of 5 pizzas, how many pizzas per group? The answer is 12 divided by 5.
- If you have 12 fifteenths, and share them into groups of 5 fifteenths, how many fifteenths per group? The answer is 12 divided by 5
You can easily check that the standard method gives the same answer.
In full detail, this method for dividing fractions looks like this :
- Convert both fractions so that they are over a common denominator.
- Divide the numerators of the two fractions.
I’ll illustrate this with the original example I gave above.
If this were the standard method kids were taught to divide fractions, we would teach
- For addition, subtraction and division, put the fractions over a common denominator and combine
- For multiplication, multiply top and bottom
then it’s possible that fraction arithmetic would be easier to grasp all round.
Or it might not. For every student who struggles with the ‘standard method’ of fraction division, there will probably be five who are greatly relieved that it doesn’t involve common denominators. Nor would I particularly recommend teaching both methods to an entire class and letting them pick for themselves. Although it’s worth knowing that many mathematical problems will bow to several different methods, there’s also the danger that different methods, shakily memorized, will combine confusedly in the pupil’s mind and completely mess up their ability to work with fractions.
Instead, I’d recommend
- Keep this method in mind for the occasional student who just doesn’t “get” the standard method for fraction division, but has no trouble with common denominators.
- Also, show it to those students bright and interested enough that they will benefit from being exposed to new approaches to familiar problems.