Last week, I got to help my son learn subtraction with borrowing. He’s already learned how to subtract two-digit numbers when borrowing is not needed, as you can see from the picture below.
In case you’re wondering about the rocket in “22-13”, let me explain. One way to work out, say, 7-4 is to count four steps backwards from 7, for example, using four fingers to mark off the four steps. Once, a long time ago, I asked him what 7-4 was, and he counted backwards “7; 6,5,4,3” and got the right answer. When I asked him 5-4, again, he got it : “5; 4,3,2,1”. What about 4-4? Again, you count backwards : “4; 3,2,1,0”.
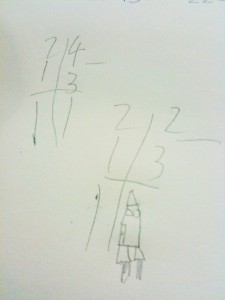
But what about 3-4? Naturally, he applied the same method, and said :
“three : two, one, zero, blast off”
So, for him, the number before zero is “blast off”. I was even more delighted when, a few weeks later, he counted even further backwards :
“…, two, one, zero, blast off, two blast off, three blast off, …”
So, “blast off” numbers are the names he gives to negative numbers. This is perfectly fine. He’s grasped part of the concept of negative numbers (way early for a grade 1 kid). Later, at the right time, someone can teach him the correct terminology. In the meantime, let him run with the terminology he’s invented.
My advice : never squash comprehension with semantics.
Anyway, I wanted to teach him subtraction with borrowing. I asked him to work out 24-13, and he got it. Then I asked him for 22-13, and he wrote what you see in the picture at the right. I’m not sure what to call his answer. Maybe BlastOffTeen or Rocketeen something. His answer is correct, in its way. If seventeen is 10+7, BlastOffTeen is 10+(Blast Off), that is, 10+(-1), which does in fact equal 9.
Of course, it wouldn’t do to leave him drawing rockets on his math quizzes!
To perform two-digit subtraction with borrowing, there are a number of non-trivial skills that must be mastered.
- The student must know to write the numbers in neat columns
- The student must know to subtract the ones digits first – more on this in a few paragraphs
- The student must be able to tell whether or not they need to borrow
- The student must know how to borrow from the tens column into the ones column
- And of course, the student needs to know how to subtract the resulting columns.

Fortunately, my son had learned a few of these skills already in school. The main one lacking was recognising when to borrow. I fixed that by teaching him the rule (borrow if the top number is less than the bottom number), working through some exercises with him, and then setting him an exercise designed to help specifically with that step. I wrote some subtraction sums, and asked him simply to circle the ones that need borrowing. There was no point boring him by asking him to complete the subtractions. The skill he specifically needed help with was recognising the need to borrow, not the borrowing or the subtraction itself. By focusing in this way, he got more practice of exactly the kind he needed.
I quizzed him again in the morning, to make sure he remembered. He was fine – this doesn’t mean the quiz was not needed – the practice was intended to reinforce the skills taught the previous evening as much as to test whether they had been learned.
Later in the week I asked my wife whether he was still doing fine – apparently he is. I should probably quiz him over the weekend with a few subtraction sums, some with borrowing and some without, just to make absolutely sure.
In the whole process, I learned a few things about how kids learn math.
First, bad habits can creep in that make life difficult later. When a student first learns two-digit subtraction with no borrowing, they might do the tens column first, or the ones column first. Whichever they do, it will quickly become a habit as they enjoy the reinforcement that repeated correct answers will give. If that habit is to do the tens column first, then they will later have to break that habit when the time comes to borrow. The new skill will become just that much harder to pick up. It’s worthwhile, well before borrowing enters the lesson plans, to ensure that students perform their subtraction from the ones digit up, not from the tens digit down. The same applies to addition as well.
Some people advocate starting from the higher digits and working down. This is good for speed mental arithmetic, but it requires backtracking whenever borrowing (or carrying) is needed. The algorithm is more complicated. Any extra complication in grade 1 is needless complication. Any procedures or algorithms taught at this level (perhaps, indeed, at any level) must be as simple and step-by-step as possible.
Second, it’s extraordinarily useful to break down this complex skill (yes, it is complex) into its simplest components, and ensure via targeted exercises that the child masters each simple component individually. Any single missing component will look like a failure to comprehend the entire method. A student who appears to not know how to subtract may only need help with a small part of the process. Until you sit down with them to identify where their misunderstanding is, and give this targeted help, their assessment of their own skill (and their confidence) will suffer.