Dinosaur Dodger Tips and Strategy

I recently uploaded a game I call “Dinosaur Dodger“. It’s based on an interesting paradox I read about on this blog, by an economist who has authored a number of good books. The paradox is called the “Paradox of the Absent Minded Driver”. It goes like this : imagine a driver, driving home along a highway. They need to take the second exit to get off, but for some reason they can’t recall which exit they are at when they get to an exit.

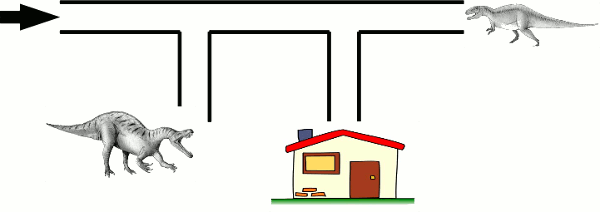
Since the two exits are identical, and since the driver can never recall, when they reach an exit, whether they’ve already passed one, the only way to have any chance of getting home is to choose randomly whether or not to turn.

If their probability of going straight is P, then, to get home,

• At the first exit, they must go straight – they have a probability of P of doing that.
• At the second exit, they must turn – they have a probability of 1-P of doing that.
• Therefore, their chance of getting home is P x (1-P) = P – P²

To make this chance as big as possible, the driver decides to choose P=1/2. A coin flip at each intersection. That’s still only a 1/4 chance of getting home, but any other P is worse. For example, if they choose either P=1 (always go straight) or P=0 (always turn), their chance of getting home is zero – in the first case because they never turn, in the second case because they always turn too soon.

Anyway, suppose the driver gets his coin ready, and starts to drive. Then he gets to an intersection, and thinks : “hang on, this is more likely to be the first intersection – I always reach the first intersection on every trip, but I only reach the second intersection on half my trips”. In fact, there’s a 1/3 chance he’s at the second intersection, and a 2/3 chance he’s at the first. So he says “All right, I’ll go straight with probability 3/5, and only turn with probability 2/5”. That way, his chance of getting home is 22/75 – almost 30% instead of 25%.

The paradox is this. He already knew, when he was starting his trip, that he would reach the first intersection – so arriving there gives him no new information! How could he come to a different logical conclusion?

Now Dinosaur Dodger is not based precisely on this paradox. Instead of one driver driving home with one strategy, there’s an explorer on a jungle track, receiving advice from a different player at each turn-off. This is quite a different conundrum from the Absent-Minded Driver Paradox. Since you are not alone in advising the explorer, your best strategy in Dinosaur Dodger depends on what everyone else is doing. Unfortunately, you don’t know exactly what that is – though perhaps you can get some clue from the high scores table.

Suppose that, on average, the other drivers are going straight with probability Q. If you decide to go straight with probability P, then your chance of getting the explorer back home is (P + Q – 2PQ)/(2-Q). If you can guess Q, then you can substitute Q and different values of P into that formula, to see how to get the most explorers home. I’ll give some examples so you can test if you are working this out properly.

• Suppose you think that Q=1/4, and you try P=1/4. Then the explorer gets home with probability (1/4 + 1/4 – 2 x 1/4 x 1/4) / (2 – 1/4) = 3/14, or only about 21%.
• On the other hand, if you think Q=1/4 and you try P=3/4, then the explorer gets home with probability (1/4 + 3/4 – 2 x 1/4 x 3/4) / (2 – 1/4), which is 5/14, or about 36%. Clearly, if you think Q=1/4, it is better to choose P=3/4 than P=1/4.

If you think Q=1/2, then, amazingly, it doesn’t matter what you choose! This is because, when Q=1/2, the explorer gets home with probability (P + 1/2 – P)/(3/2), which is 1/3 no matter what P is!

Hmm… that’s probably more than enough advice from me about the best strategy to use in Dinosaur Dodger. I wouldn’t want to spoil the game! And I’ve given enough information already for a clever spark to figure out the best strategy all by him or herself.