I’ve been reading this book, by Scott Adams, the author of Dilbert. Inside, I found a probability puzzle!
Scott Adams talks about Volleyball games, and how he noticed that the team that reaches 17 first usually wins. (A win in volleyball is 25 points.)
The probability puzzle is: what, exactly, is the chance of this happening? Scott Adams probably doesn’t realize he’s posed a probability puzzle, but he has!
Here’s how I solved it. If you want to have a crack at it yourself, stop reading now, and come back later.
I imagined that the outcome of a rally is decided, effectively, by random chance – team A wins p of the time, and team B wins 1-p of the time. For simplicity, I’ll write 1-p as q sometimes.
First I worked out Pn,k, the chance that team B has k points when team A scores their nth point.
This is really easy to work out – the simplest method is to visit Wikipedia and read about the Negative Binomial distribution. There you’ll find a simple formula for Pn,k, namely
Pn,k = n+k-1Ck pnqk
Next, I said Qn,k is the chance that team A gets n points before team B gets k. For example, Q25,25 would be the chance that team A wins the volleyball match.
Qn,k is the sum of Pn,i as i ranges from 0 to k-1. There may be a way to convert this sum into a simple formula, but I was going to ask a computer to do the heavy lifting anyway, so I didn’t bother.
Next, I said Rn,m is the chance that team A gets m points first, and then gets to n points first.
When team A gets to m points first, team B could have any number of points from 0 to m-1. The chance of each of these is given by the Pn,k. Then, for A to get to n points before B, they need another n-m points before B can clinch another n-k. Since m is bigger than k, you’d think this would be easy. Whatever it is, it’s given by Qn-m,n-k
To find Rn,m we can add the products Pm,k × Qn-m,n-k as k ranges from 0 to m-1.
R17,25 is not quite the answer to Scott Adams’ puzzle, because we don’t really care which team wins.
Rn,m depends on the chance of A winning, which is p. We can say Rn,m = Rn,m(p). The answer to the puzzle is Sn,m = Rn,m(p) + Rn,m(1-p).
Each formula given above is a relatively simple sum, although disentangling the sums into a single formula involving p might be quite difficult.
It turns out that S17,25 is actually very high. The lowest it gets is 80.9%, when the teams are perfectly matched.
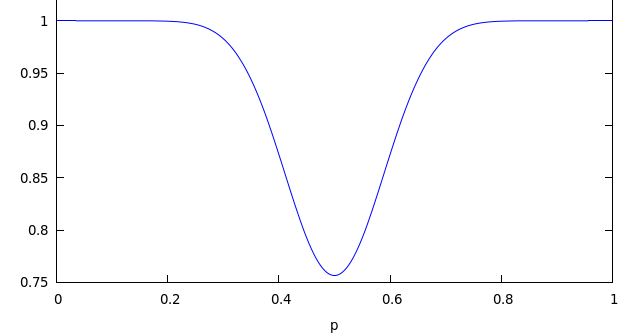
Here’s a graph of S17,25 or different values of p:
As you can see, even if the teams are slightly mismatched, the probability of confirming the Dilbert author’s observation shoots up dramatically. It’s no wonder then.
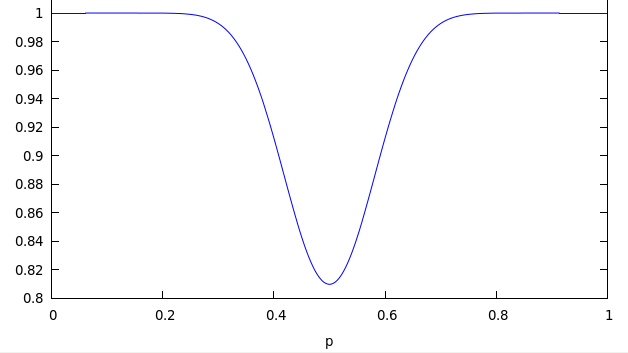
In fact, you can often pick the winner as soon as one of the teams reaches 13 points. Here’s the graph of S13,25