By Michael Hartley
Times tables require a lot of memory work, no doubt about it. However, if you thought that memory work had to be just drill after drill after boring drill, there's good news for you here!
Psychologists agree that repetition is one key to memory. The good news is
- It's not the only key
- Repetition need not be boring
Another key to memory is recognising patterns. On this page I'll show you how to open up for the kids in your care the patterns hidden in the times tables. This way,
- Memorizing the times tables will become a much easier task of remembering patterns.
- Even before the tables are memorized, children can use the patterns to work out some sums in their heads.
- This will make games like Times Tables SNAP and other times table games more fun, as they succeed more often.
Over the next few weeks I plan to upload specific tips for specific times tables. So far, I've made available
- Tips for the Five Times Table.
- Tips for the Six Times Table.
- Tips for the Seven Times Table.
- Tips for the Eight Times Table.
- Tips for the Nine Times Table.
- Tips for the Eleven Times Table.
- Tips for the Twelve Times Table.
The First Pattern
"Everybody Knows" that 16 times 88 is the same as 88 times 16. Don't they?
As educators or parents, we should never take for granted that our kids will pick this up. It's not obvious that multiplying one way is the same as multiplying the other way. It's something kids must be taught. The following exercise can help.
Choose a multiplication sum to learn. I'll use 3x7.
Ask the child to work out 3x7. Then ask him or her to work out 7x3. You could let him or her use a calculator, or better still, arrange some beads or buttons into 3 groups of 7, then 7 groups of 3.
Get a blank piece of paper, and ask the child to draw three rows of 7 circles, say something like this.
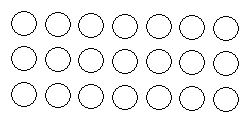
Ask the child how many circles there are, drawing attention to the three rows of seven that he or she has just drawn. Say something like So, three times seven is twenty-one
Then, draw lines to split the three rows of seven into seven columns of three.
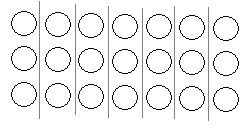
Ask the child how many columns there are, and how many in each column, then say so seven times three is the same number! It's also twenty-one, just like three times seven! Seven times three is three times seven!
Repeating similar exercises a few times will help the child deduce the general pattern. This will almost halve the amount of memorizing that your kid needs to do.
Patterns in the Digits
Each times table has a pattern in its digits. You can help your child see some of these patterns using the following exercise. I'll use the seven times table as an example, since that one is often harder for kids to learn. For other tables, the patterns that come out are even more obvious.
The first step is to write out the times table you want to help the child with. Believe it or not, it may help to go a bit beyond twelve times.
| 1 x 7 = 7 |
| 2 x 7 = 14 |
| 3 x 7 = 21 |
| 4 x 7 = 28 |
| 5 x 7 = 35 |
| 6 x 7 = 42 |
| 7 x 7 = 49 |
| 8 x 7 = 56 |
| 9 x 7 = 63 |
| 10 x 7 = 70 |
| 11 x 7 = 77 |
| 12 x 7 = 84 |
| 13 x 7 = 91 |
| 14 x 7 = 98 |
| 15 x 7 = 105 |
| 16 x 7 = 112 |
| 17 x 7 = 119 |
| 18 x 7 = 126 |
Then, draw another two columns. In the second new column, ask the child to write out just the 'ones' digit of each product. You should get something like this :
| 1 x 7 = 7 | 7 | |
| 2 x 7 = 14 | 4 | |
| 3 x 7 = 21 | 1 | |
| 4 x 7 = 28 | 8 | |
| 5 x 7 = 35 | 5 | |
| 6 x 7 = 42 | 2 | |
| 7 x 7 = 49 | 9 | |
| 8 x 7 = 56 | 6 | |
| 9 x 7 = 63 | 3 | |
| 10 x 7 = 70 | 0 | |
| 11 x 7 = 77 | 7 | |
| 12 x 7 = 84 | 4 | |
| 13 x 7 = 91 | 1 | |
| 14 x 7 = 98 | 8 | |
| 15 x 7 = 105 | 5 | |
| 16 x 7 = 112 | 2 | |
| 17 x 7 = 119 | 9 | |
| 18 x 7 = 126 | 6 |
Ask the child to read out the numbers just written. Perhaps make up a song to go with the numbers. There is a pattern here that should become clear to a child familiar with counting backwards by threes, or which will become familiar anyway with sing-song repetition.
Next, make the last empty column a 'tens-and-hundreds' column.
| 1 x 7 = 7 | 0 | 7 |
| 2 x 7 = 14 | 1 | 4 |
| 3 x 7 = 21 | 2 | 1 |
| 4 x 7 = 28 | 2 | 8 |
| 5 x 7 = 35 | 3 | 5 |
| 6 x 7 = 42 | 4 | 2 |
| 7 x 7 = 49 | 4 | 9 |
| 8 x 7 = 56 | 5 | 6 |
| 9 x 7 = 63 | 6 | 3 |
| 10 x 7 = 70 | 7 | 0 |
| 11 x 7 = 77 | 7 | 7 |
| 12 x 7 = 84 | 8 | 4 |
| 13 x 7 = 91 | 9 | 1 |
| 14 x 7 = 98 | 9 | 8 |
| 15 x 7 = 105 | 10 | 5 |
| 16 x 7 = 112 | 11 | 2 |
| 17 x 7 = 119 | 11 | 9 |
| 18 x 7 = 126 | 12 | 6 |
Reading the numbers in the tens-and-hundreds column over and over, and giving some rhythm to it,
will help the child "see" the rhythmic pattern in the numbers. Especially since the rhythm is the same as for the 'ones' digits. Compare
7, 8, 9, 9, 10, 11, 11, 12, 13, 14, ...
with
7, 4, 1, 8, 5, 2, 9, 6, 3, 0, ...
Each times table has its own "rhythm" or pattern. In each case, the patter for the ones digit is related to the pattern for the tens-and-hundred's digit. In the near future I will give tips for each individual times tables on this site. I'll explain the pattern to each one as best I can, but there's nothing like having a child discover some mathematical truth or beauty of their very own!
Less than squares
There's a simple rule for multiplying numbers that are two apart, such as 3 times 5, or 8 times 10. This exercise will help your children to learn the rule for themselves.
First, get them to complete this worksheet :
| 1 x 3 = | 2 x 2 = | ||
| 2 x 4 = | 3 x 3 = | ||
| 3 x 5 = | 4 x 4 = | ||
| 4 x 6 = | 5 x 5 = | ||
| 5 x 7 = | 6 x 6 = | ||
| 6 x 8 = | 7 x 7 = | ||
| 7 x 9 = | 8 x 8 = | ||
| 8 x 10 = | 9 x 9 = | ||
| 9 x 11 = | 10 x 10 = | ||
| 10 x 12 = | 11 x 11 = |
They should get something like this :
| 1 x 3 = | 3 | 2 x 2 = | 4 |
| 2 x 4 = | 8 | 3 x 3 = | 9 |
| 3 x 5 = | 15 | 4 x 4 = | 16 |
| 4 x 6 = | 24 | 5 x 5 = | 25 |
| 5 x 7 = | 35 | 6 x 6 = | 36 |
| 6 x 8 = | 48 | 7 x 7 = | 49 |
| 7 x 9 = | 63 | 8 x 8 = | 64 |
| 8 x 10 = | 80 | 9 x 9 = | 81 |
| 9 x 11 = | 99 | 10 x 10 = | 100 |
| 10 x 12 = | 120 | 11 x 11 = | 121 |
If you read this table row by row, you'll quickly notice a pattern. The product of numbers which are two apart is always one less than the square of the number in between. To check whether your child has understood the pattern, you could show them this table of squares, and ask them questions like What is 14 times 16? or What is 15 times 17? Once they've understood this pattern, these will be easy to work out. Then, it may be worth posting the table of squares up on the wall of the classroom or dining hall or child's bedroom, so they are exposed to it every day.
There are other patterns similar to this one. Try, for example, the following exercise. Can you spot the pattern?
| 0 x 4 = | 2 x 2 = | ||
| 1 x 5 = | 3 x 3 = | ||
| 2 x 6 = | 4 x 4 = | ||
| 3 x 7 = | 5 x 5 = | ||
| 4 x 8 = | 6 x 6 = | ||
| 5 x 9 = | 7 x 7 = | ||
| 6 x 10 = | 8 x 8 = | ||
| 7 x 11 = | 9 x 9 = | ||
| 8 x 12 = | 10 x 10 = | ||
| 9 x 13 = | 11 x 11 = |