By Michael Hartley
If you are looking for ready-made magic square puzzle worksheets, you can find a whole bunch on another page on this site. If you are the DIY kind, well, this page tells you the method I used to create them. Yes, the magician's secret is out! You can use this method to make as many magic square puzzles as you like!
What do you need? The ingredients for this method are quite simple. You only need
- A magic square. This will be the solution to the puzzle you make. To make a magic square, you can use the magic square recipes on this site, or better still, use the magic square generating applet.
- Two empty grids the same size as the magic square. I've created a few blank grids for you.
Then what?
Start with one of the empty grids. Begin placing check marks in some of the squares. Any squares you like will do. Soon, you'll have a row, column or diagonal that is all filled except for one cell. See the picture below, for example.
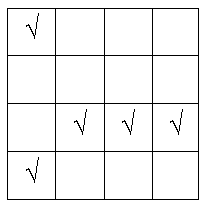
The next step is to complete that row, column or diagonal. However, instead of filling the last cell with a check mark, write a cross there instead.
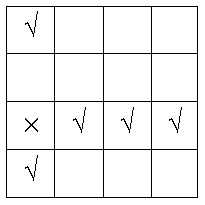
If this almost fills another row, column or diagonal, then once again you write a cross to fill the last cell.
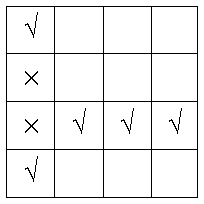
Otherwise, you continue choosing cells to write check marks. In summary, you keep doing these two steps until the grid is completely filled.
- If there is a row, column or diagonal that is filled except for one cell, fill that last cell with a cross.
- Otherwise, choose any cell you like to fill with a check mark. (Actually, you may get "better" puzzles if you deliberately try to fill rows, columns and diagonals, rather than just scattering the check marks everywhere.)
In the end, you should have something like this.
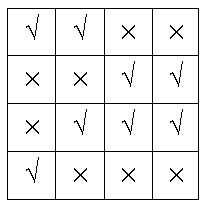
Now, you need your second empty grid, and your magic square. I'll use the magic square shown below.
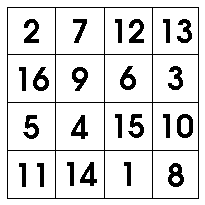
Then, you copy some of the numbers from your magic square into the empty grid. How do you know which numbers to copy? It's very simple - the first grid is your guide. You copy numbers into exactly the cells that have check marks in the first grid. Hopefully the picture below will make it clear.
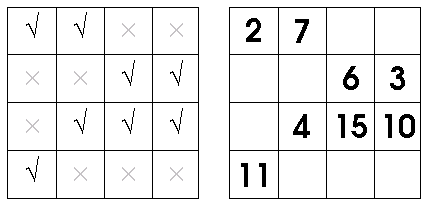
There! You have your magic square puzzle. Pass it to your students, children or friends, with the instruction -
"Fill up the grid with the numbers 1,2, 3 and so on, so that each row, column and diagonal adds up to the same number."
Enjoy!
Yours, Dr Mike...