By Michael Hartley
The 3x3 magic square is the earliest known magic square. It dates back to Chinese mythology, you can read the story here.
People normally say there is only one 3x3 magic square. In one sense this is true, in another it is not. It is true because all the 3x3 magic squares are related by symmetry. Once you have one, you can get all the others by turning or flipping the one you found.
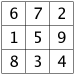
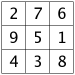
The table below shows all the 3x3 magic squares.
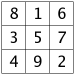 | 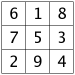 | ||
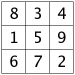 | 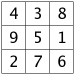 | ||
 |  | ||
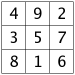 | 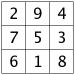 |
Have a careful look, and you'll see that each of the 3 by 3 magic squares in the grid above can be changed into its neighbors by flipping it, as if through a mirror.
Another way to change a 3x3 magic square into another is by subtracting all the numbers from 10. So, for example,
 | becomes |  |
 | becomes |  |
 | becomes |  |
 | becomes |  |
The reason there are only these 3x3 magic squares is simple enough.
First of all, since
- each row must add up to the same number,
- there are three rows, and
- 1+2+3+4+5+6+7+8+9 is 45,
Next, if you add the two diagonals and the middle column, you'll get 15+15+15=45 again. On the other hand, this is the same as adding the top row, the bottom row, and three times the middle number, so this is 15+15+middle+middle+middle. The only way to have 45 equal to 30 + 3 x middle, is if the middle number is 5.
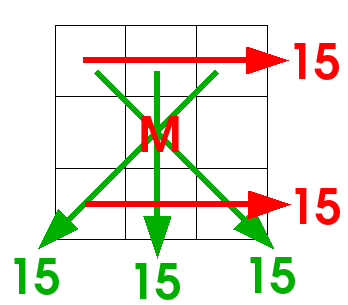
Once you know the middle is 5, you know that opposite numbers add to 10.
If 9 appears in a row or column along an edge of the square, the other numbers in that row or column have to be 2 and 4. This is because they have to add up to 6, and they can't be 1 and 5 since 5 is in the middle already. But, if 9 is in a corner, and one of the nearby corners contains 2 or 4, the other must be 8 or 6, which isn't allowed.
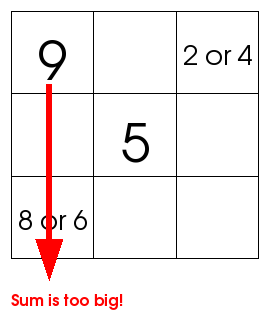
So 9 must be at the edge. The nearby corners must be 2 and 4. And 5 is in the middle. After this, it becomes an easy magic square puzzle to figure out where all the other numbers go!
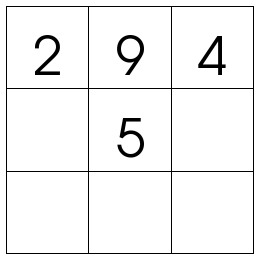
Well that's almost all for this essay on the 3x3 magic square. But did you know there's a fascinating link between the 1 to 9 game and the 3 by 3 magic square? See if you can figure out what it is!