“Everyone” knows that 3×3 + 4×4 = 5×5. This little factoid, and other Pythagorean triplets, can be the basis of a nice set of puzzles. Here’s the first. If you draw a 5×5 square on graph paper, how can you cut it up (following the lines on the graph paper) so that the pieces can be rearranged to form a 3×3 square and a 4×4 square?
This is not so hard to do. Here’s one possible solution :

Well, there’s the 5×5 square. These four pieces can be rearranged like so :
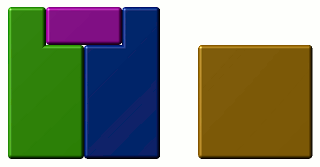
As it turns out, you can’t do it with fewer pieces than this – each corner of the 5×5 square must be in a different piece.
But there are other pairs of square numbers that add up to a square number. For example, 5×5 + 12×12 = 13×13. I managed to find a way to cut a 13×13 square into five pieces that could make a 5×5 square and a 12×12 square. Can it be done with only four? I don’t know.
And what about 7×7 + 24×24 = 25×25 ? How few pieces can you cut a 25×25 square into, so the pieces can be rearranged into a 7×7 square and a 24×24 square?
This is already enough, by way of puzzles, to keep some schoolkids occupied for a loooooong time – but there are an infinite number of pythagorean triplets, so there’s an infinite number of puzzles of this type. To find more pythagorean triplets, use these steps :
- choose two numbers, call them M and N. Make sure M is bigger than N.
- work out 2xMxN, and call this P
- work out MxM – NxN, and call this Q
- work out MxM + NxN, and call this R.
- You’ll notice that PxP + QxQ = RxR.
Then the puzzle is this : how can you chop up an RxR square, respecting the lines on the graph paper, so that the pieces can be rearranged into a PxP square and a QxQ square, using as few pieces as possible?
Note that if you allow the squares to be cut into pieces of any shape, or with straight cuts in any direction (not just parallel to the sides of the squares), then at most 7 pieces are enough to solve this puzzle. This picture (public domain, from wikipedia) shows how :
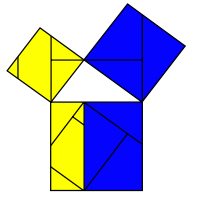
Some other formulae that give interesting puzzles :
- 1×1 + 7×7 = 5×5 + 5×5 : how can you chop up two 5×5 squares, so the pieces make a 7×7 square and a 1×1 square?
- 3x3x3 + 4x4x4 + 5x5x5 = 6x6x6 : how can you chop up a 6x6x6 cube, so that the pieces can be rearranged to make the three smaller cubes?
- 1x1x1 + 12x12x12 = 9x9x9 + 10x10x10 : how can you chop up two cubes, 9 and 10 units on their sides, and make up two cubes, 1 and 12 units on their sides?
Numbers like the last one (that can be written as the sum of two cubes in two different ways), are called “taxicab” numbers (due to an interesting incident involving two mathematicians, a hospital and taxicab number 1729). There are infinitely many taxicab numbers, but I don’t have a neat formula for them handy. If you have students who’ve exhausted the puzzles on this page, ask them to find one for you!
do u have any pythagorean puzzle like that but using a right triangle as hypothenus?