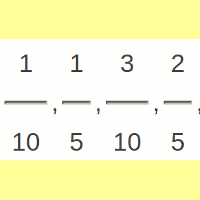By Michael Hartley
I saw a very nice fraction puzzle on a bulletin board the other day. The gist of it is something like this...
Suppose I have a job delivering papers. Each morning, as I deliver each paper (except the last one), I work out, as a fraction, how much of my round is complete. I try to simplify each fraction as much as possible.
For example, if I had 10 papers to deliver, I would work out the fractions
| 1 | 1 | 3 | 2 | 1 | 3 | 7 | 4 | 9 | ||||||||
| , | , | , | , | , | , | , | and | |||||||||
| 10 | 5 | 10 | 5 | 2 | 5 | 10 | 5 | 10 |
Notice that after four deliveries - the 1st, 3rd, 7th and 9th - the fraction can't be simplified. And that's where the puzzle comes in.
Suppose, instead of delivering 10 papers, I have to deliver a different number.
For younger kids, you can give them practice simplifying fractions. Explain the puzzle, and ask questions like...
- Suppose I deliver 9 papers, instead of 10. What fractions do I work out? How many can not be simplified? Which ones are they? Or 8 papers? Or 11, or 15?
Slightly older kids can be given a more open-ended puzzle, with questions like...
- What's the most papers I can deliver, and have four fractions that can't be simplified? Or six fractions? Or ten? Or any odd number?
- Suppose I deliver between 5 and 30 papers, and a certain number of the fractions can't be simplified. Then one day, my boss tells me I have a new customer - one extra paper to deliver. But I find there's still the same number of fractions that can't be simplified. How many customers do I have now?
- Or, for a gentle introduction to the prime numbers, ask - how many papers do I deliver if none of the fractions can be simplified?
The original puzzle was given to a grade 8 class. The question was...
- How many papers do I deliver, if the only fractions that can't be simplified come after the 1st delivery, or after prime deliveries? (Find the maximum number)
Anyway, that's all for this puzzle - you can use it either as a practice exercise in simplifying fractions, or an introduction to the prime numbers, or as an exercise in mathematical reasoning. It all depends on the level of the students you are dealing with.
Enjoy!
(By the way, the technically minded might like to know that this puzzle is related to a function called Euler's Totient Function)