By Michael Hartley
The dot-drawing game is not a join-the-dots puzzle, but rather a competitive, two-player, pencil-and-paper game. I'll explain the rules, and then explain how you can lead a class of students to use math to analyze the game. By playing, your kids will gain a sense of spatial relationships. By analyzing it, they will see how math is sometimes hidden in surprising places, and the one who uncovers math's hiding place can often use it to great advantage. It is my hope that at least some of the kids in your class will then begin to wonder - where else is math hiding in everyday things? As they find answers, some at least will gain a deep appreciation for the subject, which will stay with them for many years.
So - the rules of the game first.
- To play, all you really need is a pencil and a sheet of paper. Start by drawing some dots on the paper (between three to five dots is about the right number). If you prefer, you can print off copies of the prepared gamesheet instead.
- Players take turns to join any pair of dots with a curved or straight line. When two dots are joined, the player draws a new dot on the line. However,
- The line drawn must not cross any other line, nor pass through any other dot.
- A dot can have at most three lines coming out of it.
- A line can join a dot to itself. In this case, when counting the lines coming out of the dot, this line counts as two lines.
- The game ends when no more lines can be drawn. The winner is then the last person to draw a line.
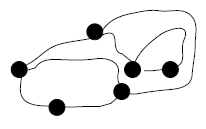
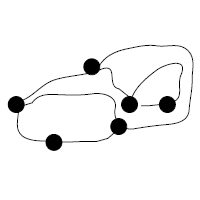
If these rules are not so clear, there's an example game shown (starting with only two dots) in the prepared gamesheet.
As kids play this game, it will improve their sense of space, as well as their strategic thinking skills. After playing a number of times, the kids should be able to figure out a few elements of strategy by themselves, for example :
- It really doesn't matter how twisty or straight the lines are drawn.
- It really doesn't matter where on a line the new dot is drawn.
- What does matter is when the edges begin to cut off regions of the board from other regions.
I suggest you pair up your class, and let them become familiar with the game, before moving on to the next stage.
Now to unlock the math hidden behind this game. You could, of course, just give the key directly to your class. However, it's much better for the children's appreciation of the math if they discover it themselves. The activities described below will help make that happen.
First, ask the class to play a few games, starting with three dots, and make a table of the results. The headings of the table should be :
- Who won, (player 1 or 2)?
- How many moves were played?
- How many dots were there at the end?
- How many edges are there joining pairs of dots?
- If you cut along the edges with scissors, how many pieces of paper would you get?
- How many dots are there with only two lines coming out?
For example, in the example game in the game worksheet, these answers would be Player 2, four moves, six dots, eight edges, and four pieces.
The players should notice some patterns after a while. In particular :
- The number of dots at the end will be three more than then number of moves played.
- The winner will be player 1 if there were an odd number of moves, player 2 if the number of moves was even.
- The number of edges is twice the number of moves.
Now ask them to play a few more games, but starting four dots, or two dots, or five dots. This will help them identify more complex patterns, and perhaps the reasons behind the patterns. For example :
- The number of dots at the end will be the initial number of dots, plus the number of moves played. This is because each move adds one dot.
- The number of edges is twice the number of moves, because each move adds two edges.
- There is even a relationship between the number of pieces of paper cut out, and the number of dots and edges - namely, pieces plus dots equals edges plus two. This is the famous Euler's formula, and it works for any collection of dots joined in a mesh by lines that don't cross each other. If some of the pupils in your class rediscover Euler's formula in this game, congratulate yourself, and ask them to test other patterns of dots, not derived from the game, to see if it still works.
You could then encourage your students to explore other questions, such as
- Do the rules they've discovered also apply in the middle of a game, or only at the end?
- How do the patterns discovered change if the rules of the game change, so that
- On each move, a player draws a dot, then three edges from that dot leading to other dots, and
- The maximum number of edges coming out of a dot is four? or five?
Let me now describe another path your class could explore. The original rules state :
This is exactly the same as saying
You could start the second exploration by getting your class to play "a new game" with the "new" rule. Soon they will click that it's actually the same game.
Another part of the rules say
You can start the second exploration by pointing out these two numbers in the rules :
- Draw a dot, then two lines coming out of it to other dots.
- A dot can have at most three lines coming out at any time.
- Draw a dot, then three lines coming out of it to other dots.
- A dot can have at most four lines coming out at any time.
- Draw a dot, then three lines coming out of it to other dots.
- A dot can have at most five lines coming out at any time.
With luck, the students will notice the following pattern :
- When the maximum number of lines per dot is less than double the number of new lines per new dot, the game stops. If it's more, the game usually goes on forever (and is not interesting). If it's equal, it depends on how the players play.