By Michael Hartley
Archimedes was an ancient Greek scientist, mathematician and philosopher. He created a great many inventions, including a kind of water pump that is still used today. Amongst his mathematical writings was one book, now lost, where he wrote about solid shapes (polyhedra) whose faces are all regular polygons, and whose corners all look the same. These shapes are now called "Archimedean Polyhedra"
If you have tiles shaped like regular polyhedra, there are a number of ways to use them to tile an infinite plane, and make each corner the same. Three of these ways use only one kind of polygon - they are the regular tesselations with triangles, squares or hexagons. You can get download links for all the graph paper on this site from my Graph Paper page.
Besides the regular tesselations, there are 8 ways to fill a plane with polygons, keeping each corner identical, and keeping everything very symmetrical. I'll explain them all here. You can download printable versions of these tesselations from the download links below
The first tesselation in the graph paper has four triangles and a hexagon around each corner. It looks like hexagons have been scattared around the plane in a regular pattern, then the gaps have been filled with triangles. In fact, there are two ways to make this pattern, because the mirror image of the pattern is a different pattern from the original. These are called the "snub hexagon tilings"
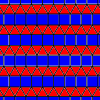
The second tesselation has three triangles and two squares around each corner. The three triangles are all next to each other, and the two squares are next to each other too, so the pattern looks very stripy, with a band of squares all in a row, then a band of triangles, then another band of squares and so on. It's called the "elongated triangular tiling"
There's another way to arrange three triangles and two squares around a corner, and this gives a much nicer pattern than the other. It's called the "snub square tiling". Look again at the snub hexagon tiling. You can see that there are two kinds of triangles. There are some that join the corners of the hexagons. The other triangles are arranged in pairs to fill the gaps between the hexagons and this first group of triangles. The snub square tiling is the same, but with squares instead of hexagons, and their corners are joined by more squares instead of by triangles.
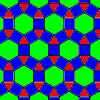
The next tiling has a fancy name - the "rhombitrihexagonal tiling". Let's break this long word down. "Rhombi" : a rhombus is a shape with four sides all the same, like a kite. A square is a kind of rhombus. This tiling has squares. "Tri" means three, and the tiling also has triangles. "Hexagonal" : it has hexagons too. This pattern is related to the snub hexagonal tiling. Remember the snub hexagonal tiling has hexagons, and tringles joining their corners together, then pairs of triangles filling the gaps? If you take the triangles filling the gaps and glue them together, you get little rhombuses filling the gaps instead. If you take out the rhombuses and twist the hexagons and the remaining triangles (keeping them joined at the corners), the rhombus-shaped holes can become square holes. Fill them withs quares, and you get the rhombitrihexagonal tiling. Here's a puzzle for you : what happens if you do the same thing with the snub square tiling?

Take some plain old square tiles, and arrange them all over the floor. Now, carefully cut off the corner of each square tile, so that it becomes a regular octogon. If you have some smaller square tiles of just the right size, you can fill the gaps with them, and get this tiling. The process of lopping off the corners of the squares is called "truncation", so this is calle dthe "truncated square tiling"
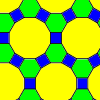
You can truncate other patterns too. In fact, you can truncate any tiling at all and get a new one. Often the new tiling won't have regular polygons as faces. If you take a honeycomb (a tesselation of hexagons) and truncate it, you get this one - the "truncated hexagonal tiling", with triangles and dodecagons. If you live in a country with dodecagonal coins (for example, the Australian 50 cent coin is a dodecagon) you can collect a whole bunch and make this pattern (except for the triangles) on the tabletop. Then, think about what you get if you take a tesselation with triangles and truncate that.

Oh no! I took a honeycomb, and chopped off the corners of the hexagons, but I chopped too much! Now, I have nice little triangular gaps, but instead of dodecagons, I have hexagons again! No matter, It's still a nice neat symmetrical pattern. It's called the "trihexagonal tiling" because it's made up of triangles and hexagons. It's the only archimedean tiling where all the lines are infinitely long. Here's a puzzle - what if you started with a square tiling, then started truncating it, but chopped off the corners too much, like I did to make this one?
As I said earlier, you can truncate any tiling at all and get a new one. The only archimedean tiling which gives you a new archimedean tiling when you truncate it is the trihexagonal tiling. If you clip the corners off the triangles and hexagons, you get hexagons and dodecagons, and leave a whole lot of square gaps. That is, you get this pattern, the "truncated trihexagonal tiling"
You can download all these Archimedean tilings (tesselations) in various sizes using the links below. Each download has all eight of these tesselations, one per page. The size given is the size of each edge of the polygons.
They might make a nice basis for an art project - asking students to color the tilings in interesting ways will, as well as letting them explore their artistic side, give them a better sense of the symmetry of each one. I'm sure that's many other ways to use these printable archimedean graph paper patterns. Why not
drop me a line and tell me what you plan to use them for, while you're waiting for them to print?