By Michael Hartley
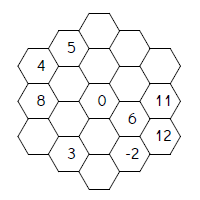
For a long time, this website has had a whole bunch of Magic Square Worksheets and other information about magic squares. Magic Hexagon puzzles are based on the same idea - arrange the numbers 1, 2, ... into a grid, with each row and diagonal adding to the same number - but this time, the grid is a hexagonal grid. Here's an example of a magic hexagon :
In some ways, Magic Hexagons are more interesting than magic squares. For example, there's only one 3x3 magic square with the numbers 1 to 9, but there are multiple 4x4 magic squares with the numbers 1 to 16, and even more magic squares with the numbers 1 to 25, and so on. As you increase size of the magic squares you're looking for, the number there are to find keeps on going up and up. Magic Hexagons are different. If you stick to the numbers 1,2,3,..., there's only one magic hexagon, the one given above.
Well, that's not quite true - there's also the simple magic hexagon below :
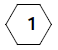
Admittedly, that's not the most interesting mathematical thing in the world, but it is a magic hexagon!
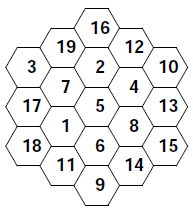
Magic hexagons become even more interesting if you decide to use other numbers, say 0,1,2,... or 2,5,8,... and so forth. If you try to use different "constant difference" sequences to form magic squares, you don't get anything new. A magic square with the numbers 1,3,5,... is just one with the numbers 1,2,3,... in disguise : to get the former from the latter, you just have to multiply each number by two, then subtract one. Not so with magic hexagons. Although there's a magic hexagon with the numbers 1,2,3,...,19, it can't be turned into a magic hexagon with the numbers 1,3,5,7...37, in fact, there isn't one with these numbers. On the other hand, there's a whole lot of magic hexagons (36 in fact) with the numbers -4,-3,-2,...,14. See how many you can find! (In counting these magic hexagons, I'm not counting rotated and flipped versions of a magic hexagon as being different from the original.)
However interesting magic hexagons are in their own right, a magic hexagon worksheet is similar in many ways to a magic square worksheet. They require almost identical skills to solve. The advantage of a magic hexagon worksheet is that your students will almost certainly never have seen one before. This webpage can generate many many different magic hexagon worksheets. Just fill in the form below, and hit 'Get A Worksheet!'.
A word of explanation about the choices here is called for. The Number Of Empty Cells controls how much work your students will have to do. If you make that number 2 or 3, there'll only be two or three numbers for them to work out. If you make it 15 or 16, you'll have a set of very difficult worksheets, some of which may have more than one solution! The Type of Worksheet determines which magic hexagons can be solutions to the puzzles.
- Only Positive Numbers mean there are no negative numbers in the worksheet. Unfortunately, there's only one magic hexagon with this property, so the solutions are all the same (but rotated and flipped into some of the 12 different possible ways).
- If you choose Mostly Positive Numbers, most of the magic hexagons will need the numbers -4 to 14, so each has four negative numbers. Since there are 36 such hexagons, you'll find more often than not that no two of the four puzzles on the worksheet have the same solution - especially since they all get randomly rotated and flipped! The 'all positive' magic hexagon will also creep in occasionally.
- If you choose Biggest Variety, about 40% of the magic hexagons will have an equal balance of positive and negative numbers, since they are filled with the numbers -9 to 9.
When you download the worksheet, you'll see that the pdf file has two pages. The first page is the actual worksheet. The second page is the answer key. Each worksheet has four magic hexagons, but if you need more, just refresh this page and download another. If you think you'll want to download the exact same worksheets later (instead of generating a new random set), bookmark this URL of the generatoe worksheet - but don't give the link to your students or they'll have the answer key!
Anyway, that's all for now. Hope it helps!